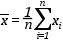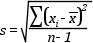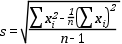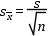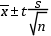A véletlen hiba a mérési eredmények átlagértéktől való eltérésében jelenik meg. A véletlen hibák eloszlását általában normális eloszlásúnak tekintjük.
A gyakorlatban mindig több párhuzamos elemzést, mérést hajtunk végre, és a mérési eredmény várhatóértékét, a mérési adatok szórását az átlagértékkel, illetve a korrigált tapasztalati szórással közelítjük.
A mérési eredmények átlagértékét n párhuzamos mérés alapján a következő módon számítjuk ki:
A korrigált tapasztalati szórást a következő egyenlettel számítjuk:
A következő képlettel egyszerűbben számolhatjuk a szórást – közvetlenül a mérési adatokból:
Az átlagérték szórása a mérési adatok szórásából számolható:
Az átlag megbízhatósági (konfidencia) intervallumát a t-eloszlás alapján számolhatjuk ki. Az mérési eredmények átlagértékének megbízhatósági intervalluma:
Attól függően, hogy milyen megbízhatósági szinten (95%, 99%, stb.) kívánjuk megadni a konfidencia intervallumot, a t tényező értékét az alábbi táblázatból az szabadsági foknak megfelelően választjuk ki.
11.1. táblázat - Konfidencia intervallumok
| Szabadságfok | t (95) | t (99) | Szabadságfok | t (95) | t (99) |
|---|---|---|---|---|---|
| 1 | 12,706 | 63,657 | 10 | 2,228 | 3,169 |
| 2 | 4,303 | 9,925 | 11 | 2,201 | 3,106 |
| 3 | 3,182 | 5,841 | 12 | 2,179 | 3,055 |
| 4 | 2,776 | 4,604 | 13 | 2,160 | 3,012 |
| 5 | 2,571 | 4,032 | 14 | 2,145 | 2,977 |
| 6 | 2,447 | 3,707 | 15 | 2,131 | 2,947 |
| 7 | 2,365 | 3,499 | 16 | 2,120 | 2,921 |
| 8 | 2,306 | 3,355 | 17 | 2,110 | 2,898 |
| 9 | 2,262 | 3,250 | ∞ | 1,960 | 2,576 |
A szórás értéke az adott analitikai eljárásra, mérési feladatra jellemző. A precizitás azonban a párhuzamos mérések számának növelésével fokozható.