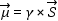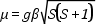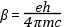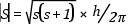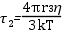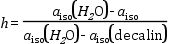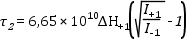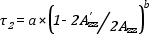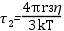Az elemi részek -atommagok és elektronok- az atomi skálán mozgást végeznek, ezért forgási impulzussal, impulzusmomentummal rendelkeznek. Elektronok esetében pálya impulzusmomentumról (L) és saját impulzusmomentumról -elektronspinről (S)- beszélünk. Mivel az elektronok e elektromos töltéssel is bírnak, ezért a mozgó töltés maga körül mágneses teret gerjeszt, így az elektronok μ mágneses momentummal (pályamágnesség és spinmágnesség) rendelkeznek. Megjegyezzük, hogy a biológiai rendszerek esetében, ahol elsősorban a szerves szabadgyökök szerepét és jelentőségét vizsgálják a biokémiai folyamatokban, a szabadgyökök strukturális felépítése miatt a pályamágnesség járuléka mindössze néhány százalék, a mágnesség gyakorlatilag spinmágnesség. Ennek megfelelően az egyszerűség kedvéért csak a spinmágnességet tárgyaljuk. A spinmágnesség arányos az impulzusmomentummal, értéke:

ahol a γ arányossági tényező: e/2mc. A mágneses momentum abszolút értéke:

ahol

A β a mágneses momentum elemi egysége, az ún. Bohr magneton, e az elektron töltése, m a tömege, h a Planck-féle állandó, c a fény terjedési sebessége. Értéke:

β_e = 9.27 x 10^-24 J/T

A formulában szereplő g (g-faktor) értéke az elektron lokális környezetétől függ, szabad elektron esetén g = 2.0023. Megjegyezzük: az atommag körül az elektronok csak meghatározott pályán keringhetnek. A lezárt alhéjon tartózkodó elektronok eredő pálya impulzusmomentuma és spinmomentuma zérus, így mágneses momentummal sem rendelkeznek. A kémiai kötésben -σ- és π-kötés- a spinek orientációja antiparallel; a kémiai kötésben általában résztvevő elektronok nem rendelkeznek mágneses momentummal. Ezen sajátosságnak megfelelően a szabadgyökök g-faktora csak 0.002 – 0.003 – mal különbözik a szabad elektron g-faktorától.

A kvantumelmélet alapvető posztulátuma, hogy a fizikai mennyiségek az atomi és molekuláris rendszerekben- energia, impulzusmomentum, mágneses momentum stb.- csak diszkrét értékekkel rendelkezhetnek; így az elektron impulzusmomentuma is csak egy elemi egység, a kvantum többszöröse lehet. Az elemi egység: h / 2π

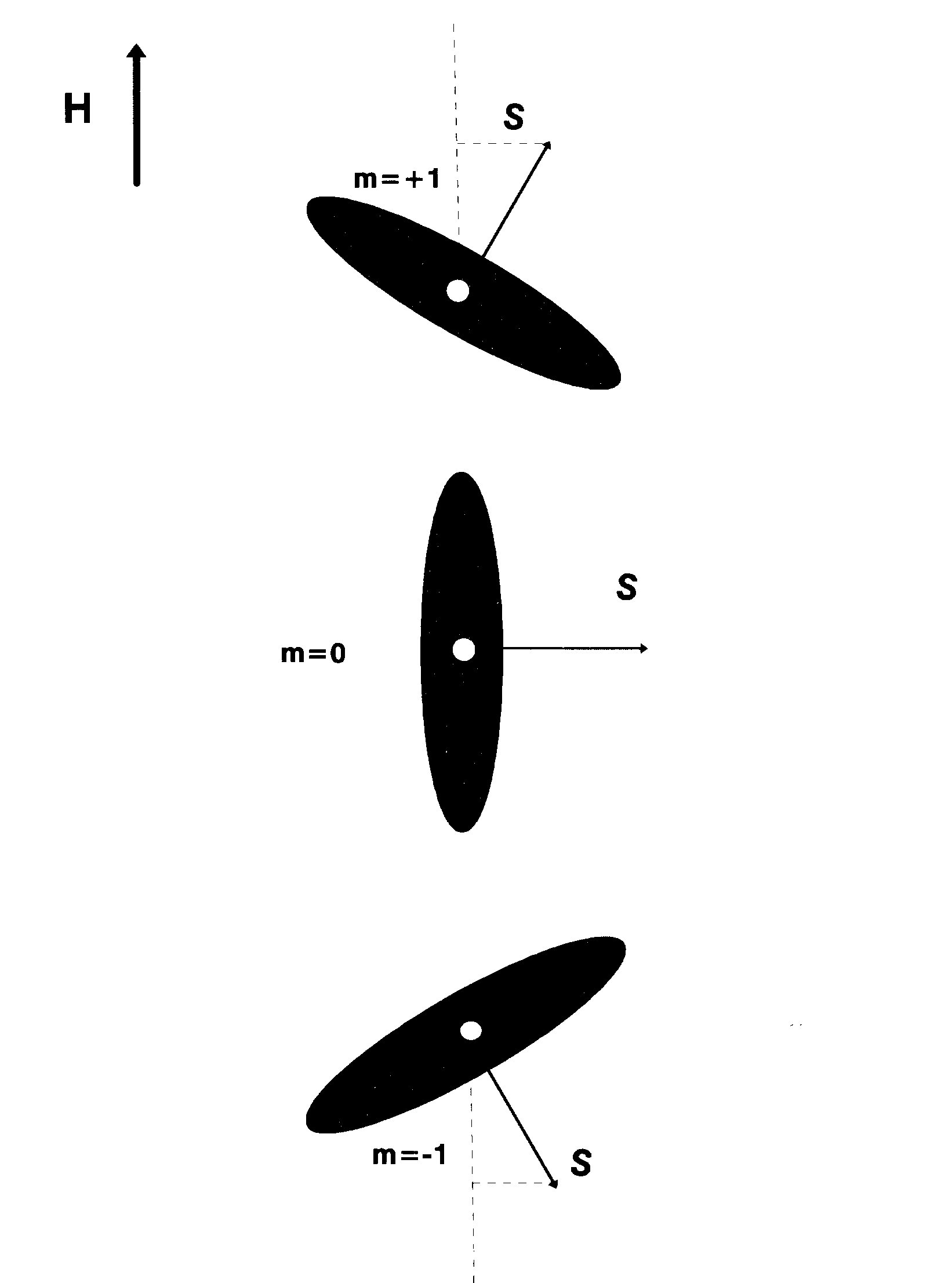
Egy forgó elemi rész (pl. elektron) impulzusmomentum vektora nem vehet fel tetszőleges orientációt egy külső térben a tér irányára vonatkoztatva (az impulzusmomentum vektormennyiség: nagysága és iránya egyaránt kvantált), az impulzusmomentum vetülete a külső tér irányára az elemi egység, h / 2π többszöröse lehet. Ha az elektronok spinje S, és m_s jelzi a vetületet egy külső H mágneses tér irányára, akkor a spinmomentum abszolút értéke:

a vetülete:

m_s * h / 2π

ahol m -s, - (s-1), ... , (s-1), s azaz összesen 2s + 1 értéket vehet fel egész számú lépésekben -s és + s között. Az iránykvantálás jelenségét Stern és Gerlach 1921-ben igazolta kísérletek segítségével. Az alábbi ábra az s = 1 esetet mutatja be:

6.1. ábra - Iránykvantálás s = 1 esetén

Mágneses tér jelenlétében az elektronok járulékos energiára tesznek szert, az energia nagysága:

E = gβHm_s

ahol m_s az elektronspin vetülete a H mágneses tér irányára. Mivel az elektronspin vetülete +1/2 vagy -1/2 lehet, ezért mágneses térben az elektronspin vagy parallel, vagy antiparallel orientációt vehet fel a tér irányára vonatkoztatva. A párnélküli elektronok járulékos energiája a két orientációnak megfelelően:

E₁ = 1/2 gβH E₂ = - 1/2 gβH

A két energia különbsége:

ΔE = gβH

A szokásos 3400 G (340 mT) mágneses tér esetén a járulékos energia:

ΔE = 6.32 x 10^-24 J,

viszont a hőmozgás átlagos energiája 300 K hőmérsékleten: kT = 4.14 x 10^-21 J, azaz mintegy három nagyságrenddel nagyobb, mint a mágneses hatásból származó járulékos energia.

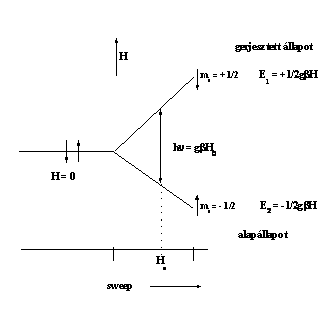
Hogy a két energiaállapot között megfigyelhessük a rezonancia jelenségét, a rendszernek energiát kell leadnia vagy felvennie. Ha a rendszert olyan elektromágneses térbe helyezzük, amelynél teljesül a

hν = gβH

feltétel, ahol ν jelenti a spektrométerben alkalmazott frekvenciát, akkor a rendszer energiacserére kényszerül a környező elektromágneses térrel. A jelenséget elektronparamágneses rezonanciának nevezzük.

6.2. ábra - Az alap és gerjesztett állapot energiaszintjei

A rezonancia jelensége csak összetartozó mágneses térerősség és frekvencia esetén mérhető. Az EPR spektrumot (az energiaelnyelés a frekvencia vagy mágneses tér függvényében) rendszerint a mágneses tér változtatásával valósítják meg.

Ha makroszkópikus méretű mintánk van, akkor az elektronok egy része az s = + 1/2 állapotban, másik részük az s = -1/2 állapotban található. A Boltzmann- eloszlás

N₊/N_- = exp (- ΔE/kT)

szerint az alacsonyabb energiájú állapot betöltöttsége (N_-) nagyobb, így rezonancia esetén nettó energiaelnyeléssel lehet számolni.

Ha az elektronok környezete eltérő, akkor a különböző g-faktorok miatt különböző mágneses térnél figyelhetjük meg a rezonancia jelenségét. Az energiacsere folyamata a rendszer és környezete között nagyon gyors (10^-6 - 10^-12 s), ezért folyamatos energiaelnyelést figyelhetünk meg. A gerjesztett állapotban lévő elektronok alapállapotba történő visszatérését irányító folyamatokat relaxációs folyamatoknak nevezzük.

6.3. ábra - N-O csoportot tartalmazó paramágneses szonda molekula spektrumának első differenciálhányadosa, abszorpciós spektruma, és integrált spektruma

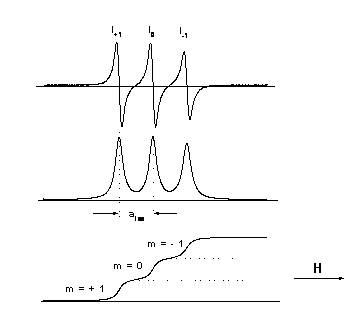
Az EPR spektroszkópiában technikai okok miatt az energiaelnyelés első differenciálhányadosát regisztrálják. A 6.3. ábra N-O csoportot tartalmazó paramágneses szonda molekula spektrumát mutatja különböző ábrázolásban (első differenciálhányados, abszorpciós spektrum, integrált spektrum). A páratlan elektron első közelítésben egy 2pπ pályán helyezkedik el az N atomon. Az N atom magspinje I = 1*h/2π, a mágneses térben három lehetséges orientációval (m_I = +1, 0, -1) rendelkezik, ennek megfelelően három EPR jel detektálható egymástól azonos távolságban (mágneses mértékegységben mérve), és azonos intenzitással.

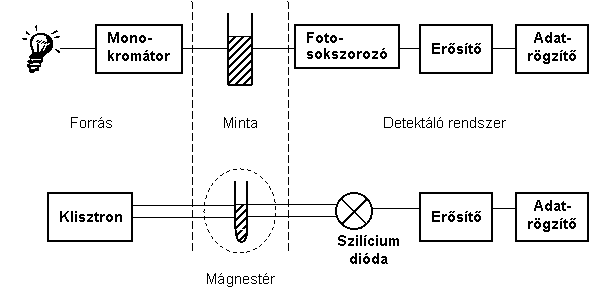
Az EPR spektrométer elvi szerkezeti felépítését tekintve nem különbözik a szokásos spektrométerektől. A 6.4. ábra együttesen vázlatosan mutatja a már tárgyalt UV-VIS spektrométer, és az EPR spektrométer működési elvét.

6.4. ábra - Az UV-VIS spektrométer és az EPR spektrométer működési elve

A lényeges eltérés abban van, hogy a vizsgálandó anyagot mágneses térbe kell helyezni, hogy a mágneses energianívók kialakuljanak. Gondoskodni kell olyan berendezésről is, amely a mágneses teret a mérés során a kívánt mértékben folyamatosan változtatja. Ennek technikai oka van, mivel a frekvencia változtatása az EPR spektrométereknél nem vagy csak nagyon nehezen valósítható meg. A vizsgálandó anyag egy speciális cellába, az üregrezonátorba kerül. Az üregrezonátor kialakítása biztosítja, hogy a szabadgyököt tartalmazó minta az elektromágneses sugárzási tér mágneses komponensének maximuma környékére kerüljön, ezzel létrejöhet a mágneses kölcsönhatás az elektromágneses sugárzási tér és az anyag mágnessége között. A rezonancia során keletkező energiaelnyelést egy szilíciumdióda érzékeli. A mérés frekvenciája a gyakorlatban használatos spektrométereknél 9.5 GHz körüli, amely 3.2 cm–es hullámhossznak felel meg.

A hullámhossz mikrohullámú technika alkalmazását kívánja meg. A rendszer az energiaelnyelést méri a mágneses tér változtatásának függvényében. Az energiaelnyelés méréséhez szükséges segédberendezéseket a megfelelő érzékenység biztosításához úgy alakították ki, hogy a spektrométer kimenő jele az energiaelnyelés első deriváltjával arányos; a mágneses tér függvényében kapott jelet hívjuk EPR spektrumnak. A jel integrálásával kaphatjuk meg az energiaabszorpciót a mágneses tér függvényében. Ha a kimenő jelet kétszer integráljuk, akkor a jel amplitúdója a mintában foglalt paramágneses centrumok koncentrációjával arányos. Megfelelő ismert paramágneses koncentrációjú anyag jelének összehasonlításával, megkaphatjuk a vizsgált minta valódi koncentrációját.

Az EPR spektroszkópiát elsősorban szabadgyökök kimutatására és azonosítására használják in vivo és in vitro, de alkalmazható biológiai rendszerek, mint például fehérjék ill. membránok szerkezetének, dinamikájának vizsgálatára is. A következőkben néhány lehetséges alkalmazás technikai lehetőségeit ismertetjük.

Spin-csapdázás

Mivel a szabadgyökök igen reakcióképes vegyületek, ezért életidejük nagyon rövid, így kimutatásuk nehézségekbe ütközik. A spin-csapdázás, idegen szóval spin trapping, lehetővé teszi egy kémiai reakció révén a primér szabadgyök átalakítását stabilisabb, rendszerint nitroxid típusú szabadgyökké. A 6.5. ábra a Fenton reakcióval keletkezett hidroxil szabadgyökök spin csapdázását mutatja be. Alkalmas spin csapda vegyület (DMPO) segítségével a befogott primér szabadgyök szerkezetének azonosítását is elvégezhetjük:

6.5. ábra - Fenton-reakcióval keletkezett hidroxil szabadgyökök spin csapdázása

Az utóbbi egy-két évtizedben számos kémiai anyagról, drogról és gyógyszerről mutatták ki, hogy szabadgyökös reakciókban vesznek részt biológiai rendszerekben. Ugyancsak számos adat mutatja, hogy normális és patológiás viszonyok között a biokémiai reakciók szabadgyökös folyamatokkal állnak kapcsolatban (pl. reaktív oxigén (ROS) és nitrogén (RNS) szabadgyökök szerepe biológiai membránokban, gyulladásos megbetegedésekben; UV, röntgen és radioaktív sugárzás kapcsán).

Spinjelölés

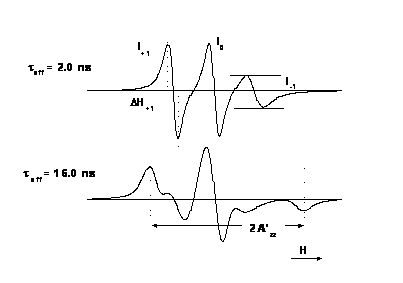
A paramágneses szonda molekulákat biológiai rendszerek dinamikájának és lokális szerkezetének vizsgálatára használják. A módszer lényege azon a megfigyelésen alapul, hogy a szonda molekulák spektrumának alakja függ a szonda molekula forgásának frekvenciájától (pontos megfogalmazással: a szonda molekula rotációs diffúziójától). A szonda molekulákat a vizsgálandó fehérje vagy makromolekula kiszemelt oldalláncához kapcsolják kovalens kötéssel. A kötés eredménye a szonda molekula immobilizálódása, amely természetesen a vizsgálandó molekulaszerkezetre jellemző. A rendszer működésekor bekövetkező konformációváltozás megmutatkozik a szonda molekula viselkedésében. Ezzel a módszerrel sikerrel vizsgálták fehérjék pl. izomfehérjék, enzimek, membránba ágyazott integrális fehérjék pl. Ca-ATPáz működését, membránok szerkezetét, permeabilitását. A csatolt ábra két eltérő forgási frekvenciájú szonda EPR spektrumát mutatja. A forgásra jellemző korrelációs időket az ábrán feltüntettük. A rotációs korrelációs idő τ₂ számítását az alábbi formula szolgáltatja:

ahol r a gömb alakúnak tekintett molekula sugara, k a Bolzmann állandó, T az abszolút hőmérséklet, η pedig a viszkozitás. A rotációs korrelációs idő alatt azt az időt értjük, amely alatt a szabadgyök vagy molekula kitüntetett tengelye egységnyi térszöggel elfordul.

6.6. ábra - A spinjelölt troponin C fehérje oldaton végzett mérés

A 6.6 ábra spinjelölt troponin C fehérje oldaton végzett mérés segítségével készült. A paramágneses molekula a súlyzó alakú fehérje molekula C-teminálisa közelében elhelyezkedő Cys-98 aminosav oldalláncához kapcsolódik. A C-terminálison van a troponin C nagy affinitású Ca kötőhelye. Kalcium távollétében a fehérje struktúra laza, így a jelölő molekula mozgékonysága nagy, amit az EPR spektrum alakja elárul (az ábra felső része). A spektrum hasonlít a vizes oldatban oldott jelölő spektrumához. Kalcium kötés hatására egy olyan konformációváltozás megy végbe, amely jelentős immobilizációval jár a Cys-98 oldallánc közelében. Ez a belső szerkezeti változás a spektrumban is megjelenik (alsó spektrum). A troponin C - ről ismert, hogy lényeges szerepe van az izomműködés szabályozásában, amely Ca kötés hatására indul meg.

A gyakorlatok célja a legáltalánosabban használt mérési technikák bemutatása, alkalmazási lehetőségeinek ismertetése Bruker ESP 300 E típusú spektrométerrel, EPR spektroszkópiai mérések elvégzése standard mintákon, a detektált eredmények kiértékelése.

Segédlet a számítások elvégzéséhez

Polaritás kiszámítása. A polaritás kiszámítására a következő összefüggést használják:

ahol h a polaritásra jellemző paraméter, a_iso -k pedig a megfelelő anyagok izotróp csatolási állandói.

Rotációs korrelációs idő kiszámítása. Gyors forgás esetén (τ₂ < 5 nsec) a rotációs korrelációs idő kiszámítására a következő egyszerű összefüggés használható:

ahol ΔH₊₁ az első átmenet csúcs-csúcs közötti távolságát jelenti Gauss-ban mérve a derivált spektrumban, I₊₁ és I_-1 az első és harmadik átmenet amplitúdóját. A korrelációs időt sec -ban kapjuk.

Lassú mozgás (τ₂ > 5 nsec) esetén a Goldmann-közelítés alkalmazható a rotációs korrelációs idő kiszámítására:

ahol a = 5.4 * 10^-10 sec, b = - 1.36

2A’_ZZ ill. 2A_ZZ pedig az EPR spektrumból kimérhető hiperfinom csatolási állandókat jelenti. 2A_ZZ felel meg az u.n. rigid limit -nek, amelynél a rendszer makroviszkozitása a végtelenhez közelít, esetünkben a MSL label liofilizált fehérjéhez kötött.

A mikroviszkozitás kiszámítása. A mikroviszkozitás kiszámítását a Debye-formula segítségével végezzük:

ahol r a gömbalakúnak tekintett TEMPO molekula sugara (kb.1.5 Å), k a Bolzmann állandó, T az abszolút hőmérséklet, τ₂ a spektrumból számított rotációs korrelációs idő, η pedig a mikroviszkozitás.

mágneses rezonancia, impulzusmomentum, elektronspin, mágneses momentum, kvantum, iránykvantálás, g-faktor, üregrezonátor, EPR spektrum, spin-csapdázás, spinjelölés, csatolási állandó